Operations for functions: Inverse functions
 Characterizing invertible functions
Characterizing invertible functions
Characterization of invertible functions
A function \(f\) has an inverse if and only if it is injective. In that case the domain of #f^{-1}# is equal to the range of #f#.
If #f# is injective, then the equation #y=f(x)# with unknown #x# has exactly one solution if #y# lies in the range of #f# and no solution if that is not the case. This means that the function #g# with domain equal to the range of #f# and with function rule \[g(y)\text{ is the unique solution }x\text{ of }y=f(x)\] is the inverse of #f#.
The other way around: assume that #g# is the inverse of #f#, and that #x_1# and #x_2# are numbers in the domain of #f# with #f(x_1)=f(x_2)#. Then #x_1=g(f(x_1)=g(f(x_2))= x_2# has to hold, or: #x_1=x_2#. This shows that #f# is injective.
The vertical-line test for invertibility
Let #f# be a function.
- The graph of #f# meets each horizontal line at most once if and only if #f# is injective.
- The graph obtained by reflecting the graph of #f# about the line with equation #x=y# meets every vertical line at most once if and only if #f# is invertible.
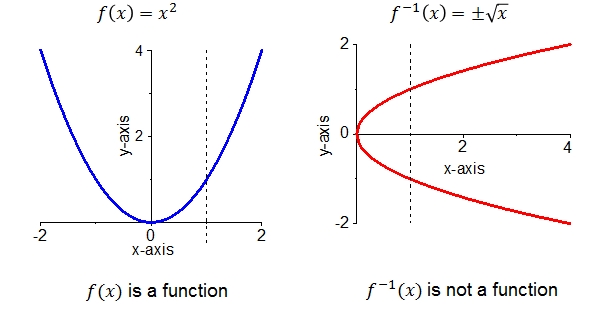
The graph of the function #f(x)=x^2# is drawn on the left and its reflection about #x=y# on the right. It is clear that the two criteria are the same: On the left, there are horizontal lines that meet the graph in two points. Therefore, #f# is not injective. On the right there are vertical lines that meet the graph in two points. Therefore, this graph is not the graph of a function; but it should be the graph of an inverse function. This shows that #f# has no inverse.
Because all five values of #f# differ, this function is injective, and hence invertible. What is the inverse of #f#?
Describe #f^{-1}# by a list of five numbers as was done for #f#.
Have a look at the values for #f # at position #j#.
#\begin{array}{rcl}
\text{the value of } f = & [5,2,1,4,3] \\
\text{where position } j = & [1,2,3,4,5] \\
\end{array}#
the inverse function #f^{-1} # swaps the positions and the values of #f#:
#\begin{array}{rcl}
\text{the new value } = & [1,2,3,4,5] \\
\text{where the position } j = & [5,2,1,4,3] \\
\end{array}#
If we sort the this list of values based on the position, we get
#f^{-1} = [3,2,5,4,1]#
Indeed, position #j# in this list is the position where #f# has value #j#.
As an example for position #1#:
#f# has at position #1# the value #5,# thus #f(1)=5#. The inverse function should undo this change, thus #f^{-1}(5)=1#.
Same way for position #2#:
Since #f(2)=2#, #f^{-1}(2)=2#.
If this list is called #g#, then #f(g(j)) = j# holds for each #j\in\{1,2,3,4,5\}#. This means that #g# is the inverse of #f# and if you first apply #f#, next #f^{-1}#, all is back into the original positions.

Or visit omptest.org if jou are taking an OMPT exam.



