Scaling functions

Operations for functions: New functions from old

Scaling functions

We will study the results of blowing up or shrinking the graph of a function in the horizontal or vertical direction.

Vertical rescaling

Let $a$ be a real number distinct from $0$ . Vertical scaling by $a$ sends the point $\rv{x,y}$ of the plane to $\rv{x,a\cdot y}$ .

Under vertical scaling by $a$ , the graph of a function $f$ is turned into the graph of $a\cdot f$ , that is, the function of $x$ with rule $a\cdot f(x)$ .

The graph of $f$ consists of all points of the form $\rv{x,f(x)}$ . Under scaling by $a$ , these points become $\rv{x,a\cdot f(x)}$ which are indeed the points of the graph of the function $a\cdot f$ .

The points of the plane stretched vertically if $a\gt0$ and shrunk vertically if $a\lt0$ . In the case $a\lt0$ the graph will also flip about the $x$ -axis (the originated graph will be the mirror reflection of $f$ about the $x$ axis). The location of the zeros of the function $f$ will be the same as well as the location of the minimums and/or maximums that will only change in terms of $y$ by the factor $a$ .

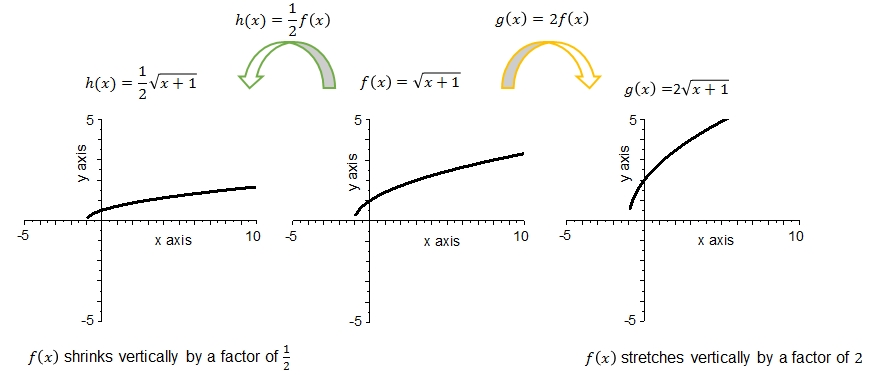
The following facts can be observed in the above graphs:

The graph of $f$ is the square root of $\sqrt{x+1}$ with zero $x=-1$ and a minimum at $f(-1)=0$ .
The graph of $h$ is the square root of $\sqrt{x+1}$ multiplied by $\frac{1}{2}$ with zero $x=-1$ and a minimum at $f(-1)=0$ .
The graph of $g$ is the square root of $\sqrt{x+1}$ multiplied by $2$ with zero $x=-1$ and a minimum at $f(-1)=0$ .

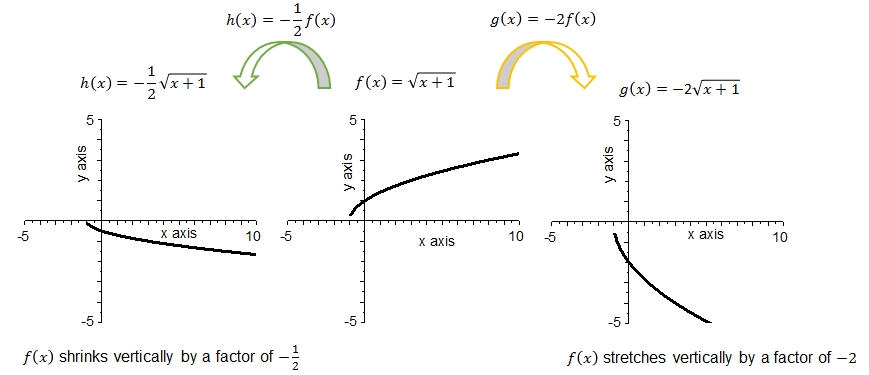
The following facts can be observed in the above graphs:

The graph of $f$ is the square root of $\sqrt{x+1}$ with zero $x=-1$ and a minimum at $f(-1)=0$ .
The graph of $h$ is the square root of $\sqrt{x+1}$ multiplied by $-\frac{1}{2}$ with zero $x=-1$ and a maximum at $f(-1)=0$ .
The graph of $g$ is the square root of $\sqrt{x+1}$ multiplied by $-2$ with zero $x=-1$ and a maximum at $f(-1)=0$ .

Horizontal rescaling

Let $a$ a real number distinct from $0$ . Horizontal scaling by $a$ sends the point $\rv{x,y}$ of the plane to $\rv{a\cdot x,y}$ .

Under horizontal scaling by $a$ , the graph of a function $f$ is turned into the graph of the function with rule $f\left(\frac{x}{a}\right)$ .

Putting $x_1=a\cdot x$ , we have $\rv{a\cdot x,f(x)}=\rv{x_1,f\left(\frac{x_1}{a}\right)}$ . This shows that the function rule of the function whose graph is obtained by the horizontal scaling of the graph of $f$ , is equal to $f\left(\frac{x_1}{a}\right)$ .

The function $f$ is shrunk horizontally if $a\gt1$ or $a\lt-1$ by a factor of $\frac{1}{a}$ and stretched horizontally if $-1\lt a\lt 1$ by a factor of $a$ with $a\neq 0$ .

In case $a\lt0$ , the graph will also flip about the $y$ -axis (the originated graph will be the mirror reflection of $f$ about the $y$ -axis). The location of the zeros of the function $f$ as well as the location of the minima and/or maxima will change, whereas in terms of $y$ the minima and/or maxima will remain the same.

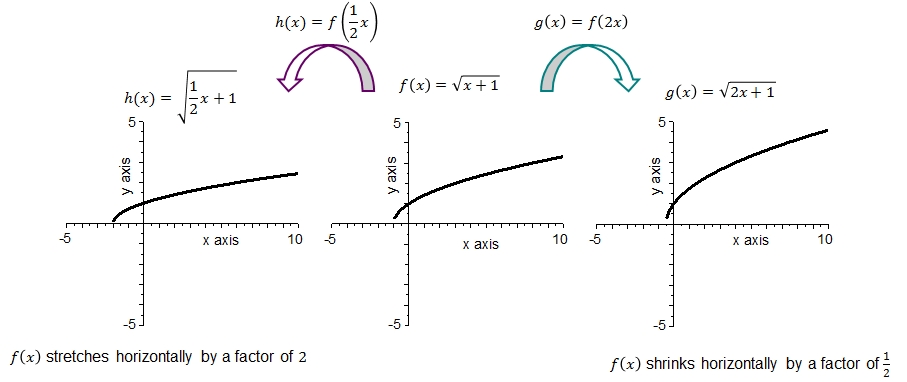
It is possible to observe the following facts from the above graphs:

The graph of $f$ is the square root of $\sqrt{x+1}$ with zero $x=-1$ and a minimum at $f(-1)=0$ .
The graph of $h$ is the square root of $\sqrt{\frac{1}{2}x+1}$ with zero $x=-2$ and a minimum at $f(-2)=0$ .
The graph of $g$ is the square root of $2x+1$ with zero $x=-\frac{1}{2}$ and a minimum at $f(-\frac{1}{2})=0$ .

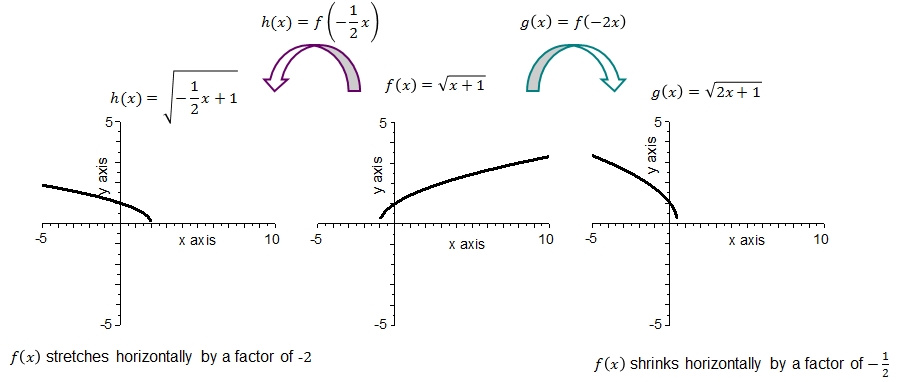
It is possible to observe the following facts from the above graphs:

The graph of $f$ is the square root of $\sqrt{x+1}$ with zero $x=-1$ and a minimum at $f(-1)=0$ .
The graph of $h$ is the square root of $-\sqrt{\frac{1}{2}x+1}$ with zero $x=2$ and a minimum at $f(2)=0$ .
The graph of $g$ is the square root of $-2x+1$ with zero $x=\frac{1}{2}$ and a minimum at $f(\frac{1}{2})=0$ .

Let $f(x)= \sqrt{x+4}$ . Below the graph of $f$ is drawn as well as its vertical scaling and horizontal scaling by $2$ .

Which graph corresponds to which scaling?

The graph of $f$ is blue.
The vertical scaling of the graph belongs to the function $2\cdot f(x) = 2\cdot\left(\sqrt{x+4}\right)$ $=2\cdot \sqrt{x+4}$ and is red.
The horizontal scaling of the graph belongs to the function $f\left(\frac{x}{2}\right) = \sqrt{{{x}\over{2}}+4}$ $={{\sqrt{x+8}}\over{\sqrt{2}}}$ and is green.

New example