Functions: Quadratic functions
 The quadratic formula
The quadratic formula
By completing the square we can rewrite the quadratic expression #ax^2+bx+c# as \[a\cdot\left(\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2-4a\cdot c}{(2a)^2}\right)\tiny.\] We use this formula to solve quadratic equations.
Discriminant and quadratic formula
Let #a#, #b#, and #c# be real numbers with #a\ne0#. The equation #ax^2+bx+c=0# can be reduced to
\[x=\dfrac{-b - \sqrt{b^2-4a\cdot c}}{2a}\lor x=\dfrac{-b+ \sqrt{b^2-4a\cdot c}}{2a}\]
The expression #b^2-4ac# is called the discriminant of #ax^2+bx+c#, and is often referred to with #D#.
With this notation \[x=\dfrac{-b - \sqrt{D}}{2a}\lor x=\dfrac{-b+ \sqrt{D}}{2a}\]
- If #D\lt 0#, then there are no solutions.
- If #D= 0#, then there is only one solution: #x=\dfrac{-b}{2a}#.
- If #D\gt 0#, then there are two solutions.
The above is also called the quadratic formula. With this formula any quadratic equation can be solved.
The reduction is as follows:
\[\begin{array}{rcl}ax^2+bx+c&=&0\\ &&\phantom{xx}\color{blue}{\text{the original equation}}\\ a\cdot\left(\left(x+\dfrac{b}{2a}\right)^2-\dfrac{D}{(2a)^2}\right)&=&0\\ &&\phantom{xx}\color{blue}{\text{the square completed, with }D = b^2-4a\cdot c}\\ \left(x+\dfrac{b}{2a}\right)^2-\dfrac{D}{(2a)^2}&=&0\\ &&\phantom{xx}\color{blue}{\text{left and right hand side divided by }a\text{ }}\\ \left(x+\dfrac{b}{2a}\right)^2&=&\dfrac{D}{(2a)^2}\\ &&\phantom{xx}\color{blue}{\text{constant term to the right hand side }}\\ x+\dfrac{b}{2a}&=&\pm\sqrt{\dfrac{D}{(2a)^2}}\\ &&\phantom{xx}\color{blue}{\text{root taken; }\pm\text{means: }+\text{ of }-}\\ x+\dfrac{b}{2a}&=&\pm\dfrac{\sqrt{D}}{2a}\\ &&\phantom{xx}\color{blue}{\text{root simplified}}\\ x&=&-\dfrac{b}{2a}\pm\dfrac{\sqrt{D}}{2a}\\ &&\phantom{xx}\color{blue}{\text{constant term to the right hand side}}\\ \end{array}\]
The quadratic formula can be used to determine the intersection points of a parabola with the #x#-axis. What does this mean for the three cases which we have just seen? We will still consider a parabola opening upwards.
If #D\gt0#, then the square root is taken from a positive number, so the equation #ax^2+bx+c=0# has two different solutions. The parabola, that is, the graph of #ax^2+bx+c#, intersects the #x#-axis twice.
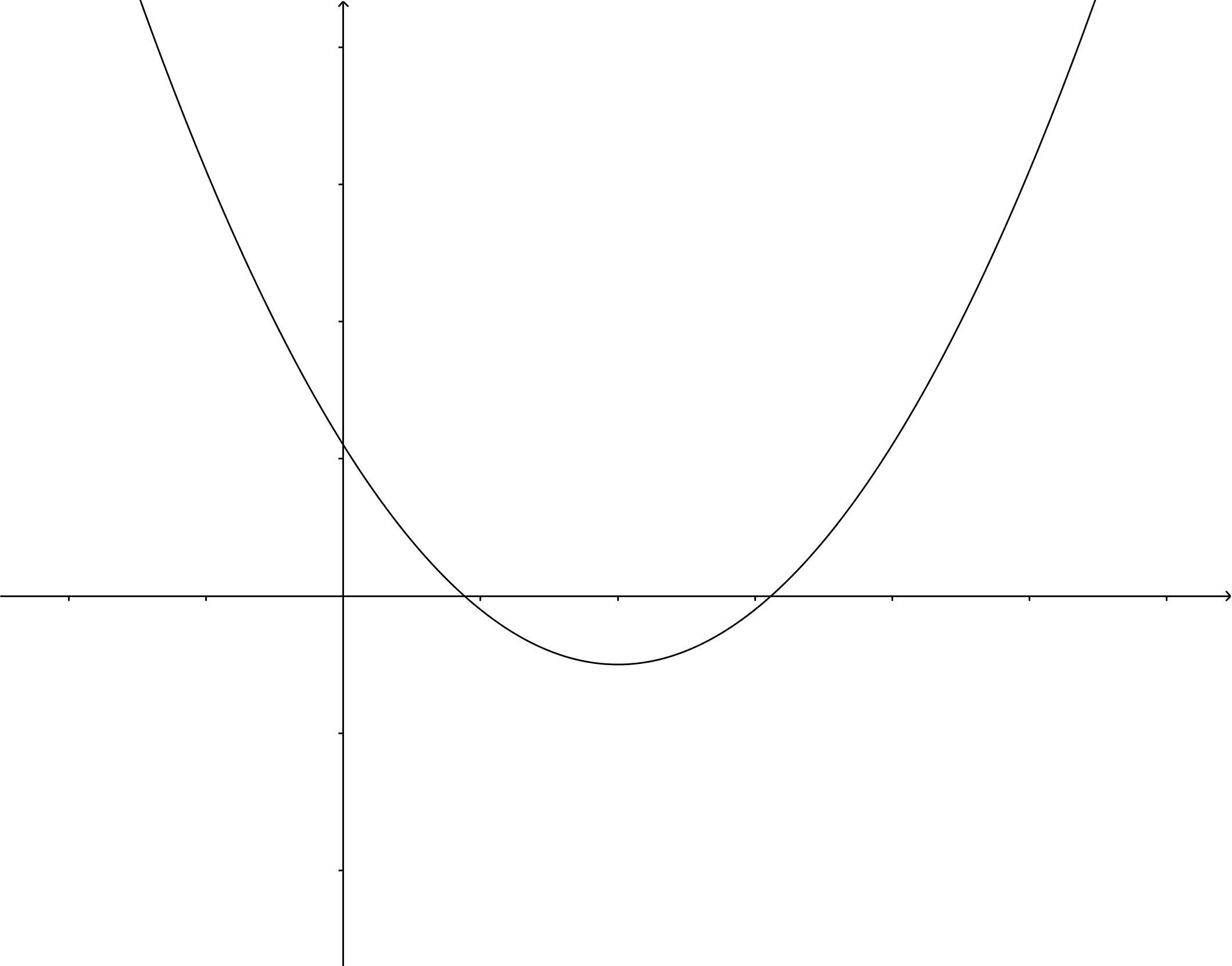
If #D\lt0#, then there are no solutions because taking the square root of a negative number does not have any real numbers as solution. The parabola will not intersect the #x#-axis.
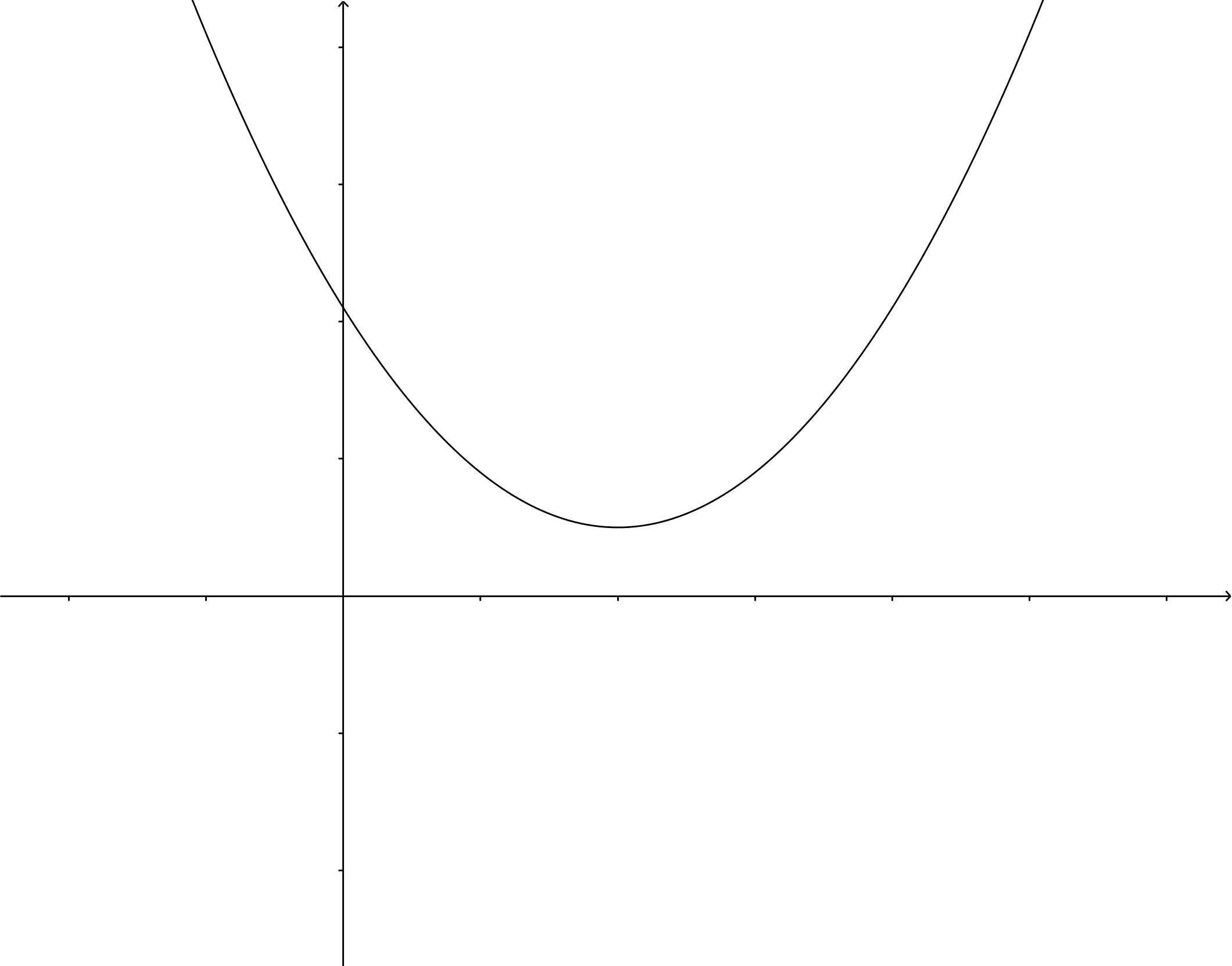
If #D= 0#, then both solutions are equal and there is only one solution: #x=\dfrac{-b}{2a}#. Here the parabola touches the #x#-axis.
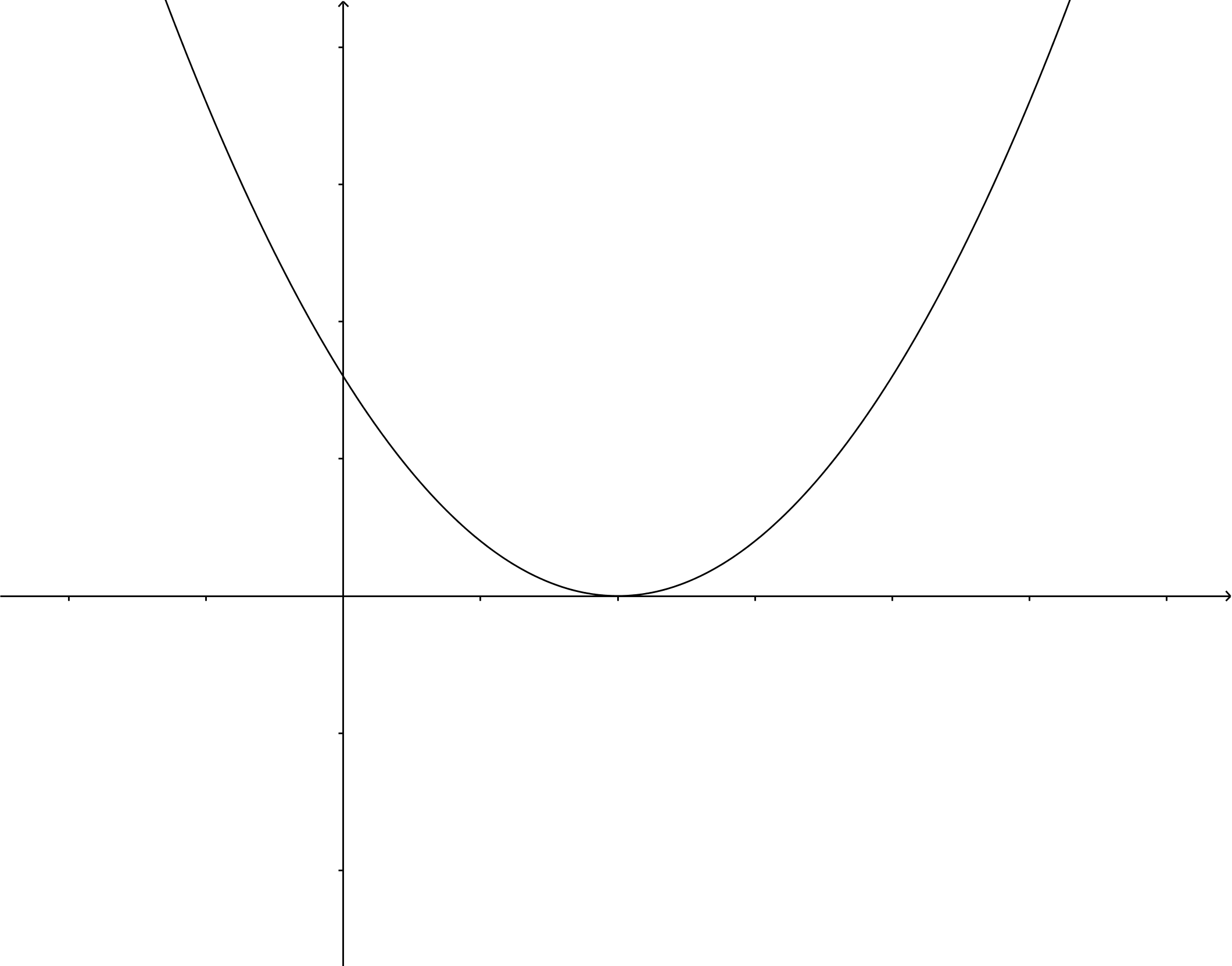
Use the quadratic formula:
\[x=\frac{-b-\sqrt{D}}{2a}\lor x=\frac{-b+\sqrt{D}}{2a}\]
with discriminant #D=b^2-4a\cdot c#.
\[\begin{array}{rcl}
a=3&b=-6&c=-{{63}\over{4}}\\
&&\phantom{xx}\color{blue}{\text{a, b and c determined}}\\
(-6)^2-4\cdot 3\cdot -{{63}\over{4}}&=&225\\
&&\phantom{xx}\color{blue}{\text{discriminant calculated}}\\
x=\frac{6-15}{6}&\lor&x=\frac{6+15}{6}\\
&&\phantom{xx}\color{blue}{\text{quadratic formula used}}\\
x=-{{3}\over{2}}&\lor&x={{7}\over{2}}\\
&&\phantom{xx}\color{blue}{\text{solution simplified}}\\
\end{array}\]The graph of the function #y=3 x^2-6 x-{{63}\over{4}}# is drawn below. The #x#-coordinates of the meeting points of the graph and the #x#-axis are the solutions to the equation.


Or visit omptest.org if jou are taking an OMPT exam.



