Hogeregraadsongelijkheden

Functies: Hogeregraadsfuncties

Hogeregraadsongelijkheden

Op dezelfde manier als we een kwadratische ongelijkheid oplossen, kunnen we ook een ongelijkheid met hogeregraads veeltermen oplossen.

Een hogeregraadsongelijkheid oplossen

	Stappenplan	Voorbeeld
	We lossen de volgende ongelijkheid op $\blue{f(x)} \gt \green{g(x)}$ waarbij $\blue{f(x)}$ en $\green{g(x)}$ polynomen zijn.	$\blue{x^6+x^3+6} \gt \green{-2x^3+10}$ (resp. doorgetrokken en gestreept) 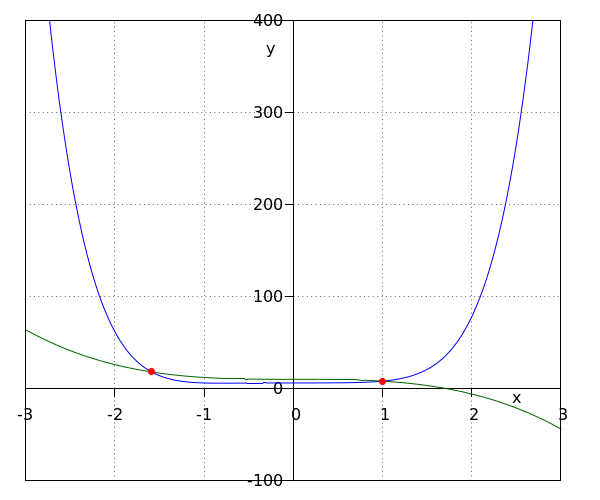De oplossing is $x \lt \sqrt[3]{-4} \land x \gt 1$ .
Stap 1	We lossen de gelijkheid $\blue{f(x)} = \green{g(x)}$ op.
Stap 2	We schetsen de grafieken $\blue{f(x)}$ en $\green{g(x)}$ .
Stap 3	Bepaal met behulp van stap 1 en 2 voor welke waarden van $x$ de ongelijkheid geldt. In een assenstelsel is de grootste grafiek degene die boven ligt.

Merk op dat dit stappenplan ook voor de ongelijkheidstekens $\geq$ en $\leq$ geldt, alleen nu horen de $x$ -waarden van de snijpunten ook bij de oplossing.

Alle of geenAls er in stap 1 geen snijpunten gevonden worden, dan zijn er twee opties voor de oplossing van de ongelijkheid.

alle punten van $x$ zijn een oplossing van de ongelijkheid. De ongelijkheid is altijd waar.
geen punten van $x$ zijn een oplossing van de ongelijkheid. De ongelijkheid is nooit waar.

Ditzelfde kan ook als in stap 1 wel een snijpunt gevonden wordt, maar dit een raakpunt is. Dan zijn ze alleen in dat punt gelijk en in alle andere punten geldt de ongelijkheid wel of niet.

Alternatief stap 2

In plaats van de grafieken te schetsen, kunnen we in stap 2 ook een aantal $x$ -waarden substitueren in $\blue{f(x)}$ en $\green{g(x)}$ om te zien op welke intervallen $\blue{f(x)} \gt \green{g(x)}$ .

Omdat slechts in de snijpunten van $\blue{f(x)}$ en $\green{g(x)}$ kan wisselen welke functie groter is, is het voldoende om links en rechts van elke snijpunt één $x$ -waarde te nemen.

In het voorbeeld hierboven en hiernaast zijn de snijpunten van $\blue{f(x)}$ en $\green{g(x)}$ de $x$ -waarden: $x = \sqrt[3]{-4}$ en $x =1$ . We kiezen nu dus een $x$ -waarde kleiner dan $\sqrt[3]{-4}$ , een waarde tussen $x= \sqrt[3]{-4}$ en $x=1$ en een waarde groter dan $1$ . Op deze manier weten we wanneer $\blue{f(x)}$ groter is dan $\green{g(x)}$ .

Voorbeeld

In het bovenstaande voorbeeld substitueren we een aantal $x$ -waarden.

$\blue f(-2)=62 \gt \green g(-2)=26$

$\blue f(0)=6 \lt\green g(0)=10$

$\blue f(2)=78 \gt \green g(2)=-6$

We lezen dan in stap 3 af dat:
De oplossing is $x \lt \sqrt[3]{-4} \land x \gt 1$ , omdat de ongelijkheid klopt voor $x=-2$ en $x=2$ .

Los $x$ op in de ongelijkheid
$x^{10}+6\cdot x^5+2\cdot x+14 \lt 2\cdot x+9\tiny$
Geef je antwoord in de vorm

$x \gt x_1\land x \lt x_2$ of $x\lt x_1 \lor x \gt x_2$ ,
$x \lt x_1$ of $x \gt x_1$ ,
$geen$ of $alle$ ,

met de juiste waardes voor $x_1$ en $x_2$ .

$x\gt -5^{{{1}\over{5}}}\land x\lt -1$

Stap 1	We lossen de gelijkheid $x^{10}+6\cdot x^5+2\cdot x+14=2\cdot x+9$ op. Dat gaat als volgt: $\begin{array}{rcl} x^{10}+6\cdot x^5+2\cdot x+14&=&2\cdot x+9 \\ &&\phantom{xxx}\blue{\text{oorspronkelijke vergelijking}}\\ x^{10}+6\cdot x^5+5&=&0 \\&&\phantom{xxx}\blue{\text{herleid op }0}\\ \left(x^5+1\right)\cdot \left(x^5+5\right)&=&0 \\&&\phantom{xxx}\blue{\text{linkerlid ontbonden in factoren}}\\ x^5+1=0 &\lor& x^5+5=0 \\&&\phantom{xxx}\blue{A\cdot B=0 \text{ dan en slechts dan als }A=0\lor B=0}\\ x=-1 &\lor& x=-5^{{{1}\over{5}}} \\&&\phantom{xxx}\blue{\text{constante ter‍men naar rechts gebracht en wortel getrokken}}\\ \end{array}$
Stap 2	We schetsen de grafieken $y=x^{10}+6\cdot x^5+2\cdot x+14$ (blauw) en $y=2\cdot x+9$ (groen gestreept).
Stap 3	We lezen nu de oplossing van de ongelijkheid af. $x\gt -5^{{{1}\over{5}}}\land x\lt -1$

Nieuw voorbeeld