Goniometrie: Goniometrische functies
 Goniometrische functies
Goniometrische functies
De sinus, cosinus en tangens worden niet alleen bij hoeken gebruikt, maar kunnen ook als functie gebruikt worden.
De sinusfunctie #f(x)=\sin(x)# is de functie die aan elk getal #x# de sinus van #x# radialen toevoegt.
Zoals we bij de eenheidscirkel gezien hebben, herhaalt de functie zich elke #2 \pi#. We noemen de sinusfunctie daarom een periodieke functie met #\blue{\text{periode}}# #2 \pi#.
De functie heeft ook een #\green{\text{evenwichtsstand}}#. Dit is het midden van de functie, oftewel de #y#-waarde die precies tussen het hoogte en laagste punt ligt. Bij de sinusfunctie is deze #0#.
Tot slot is de #\purple{\text{amplitude}}# van de functie gelijk aan #1#. Dit betekent dat de waarde van de evenwichtsstand tot aan het hoogste punt (of: laagste punt) gelijk aan #1# is.
De cosinusfunctie #f(x)=\cos(x)# is de functie die aan elk getal #x# de cosinus van #x# radialen toevoegt.
Net als de sinusfunctie is de cosinusfunctie een periodieke functie. Ook deze heeft #\blue{\text{periode}}# #2\pi#.
De #\green{\text{evenwichtsstand}}# is gelijk aan #0#.
Verder is de #\purple{\text{amplitude}}# van de functie gelijk aan #1#.
Wanneer we de cosinusfunctie vergelijken met de sinusfunctie zien we dat de grafieken sterk op elkaar lijken. Wanneer we de cosinusfunctie met #\frac{\pi}{2}# naar rechts schuiven, hebben we de sinusfunctie.
De tangensfunctie #f(x)=\tan(x)# is de functie die aan elk getal #x# de tangens van #x# radialen toevoegt.
Net als de sinus- en de cosinusfunctie is tangensfunctie een periodieke functie. De #\blue{\text{periode}}# is gelijk aan #\pi#.
De tangensfunctie heeft verticale asymptoten bij #x=\frac{\pi}{2}+k \cdot \pi#, waarbij #k# een geheel getal is, zoals bij de #x#-waarden #\frac{\pi}{2}#, #\frac{3 \pi}{2}# en #\frac{5 \pi}{2}#, maar ook bij #\frac{-3 \pi}{2}#.
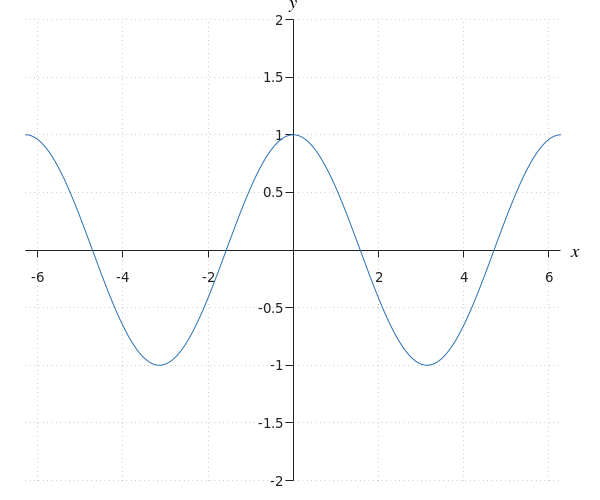
Van welke functie is deze grafiek?
We zien een functie met evenwichtsstand gelijk aan #0#, periode #2 \pi# en amplitude #1#. Verder gaat de functie door het punt #\rv{0,1}#. Dat betekent dat de functie gelijk is aan #f(x)=\cos(x)#.

omptest.org als je een OMPT examen moet maken.



