Approximation

Rules of differentiation: Applications of derivatives

Approximation

Assume that we are interested in the numerical value of $\sqrt{1.1}$ . We know that the tangent line at $x=1$ to the graph of $\sqrt{x}$ provides a good approximation. The graph of the square root and the tangent line are drawn below.

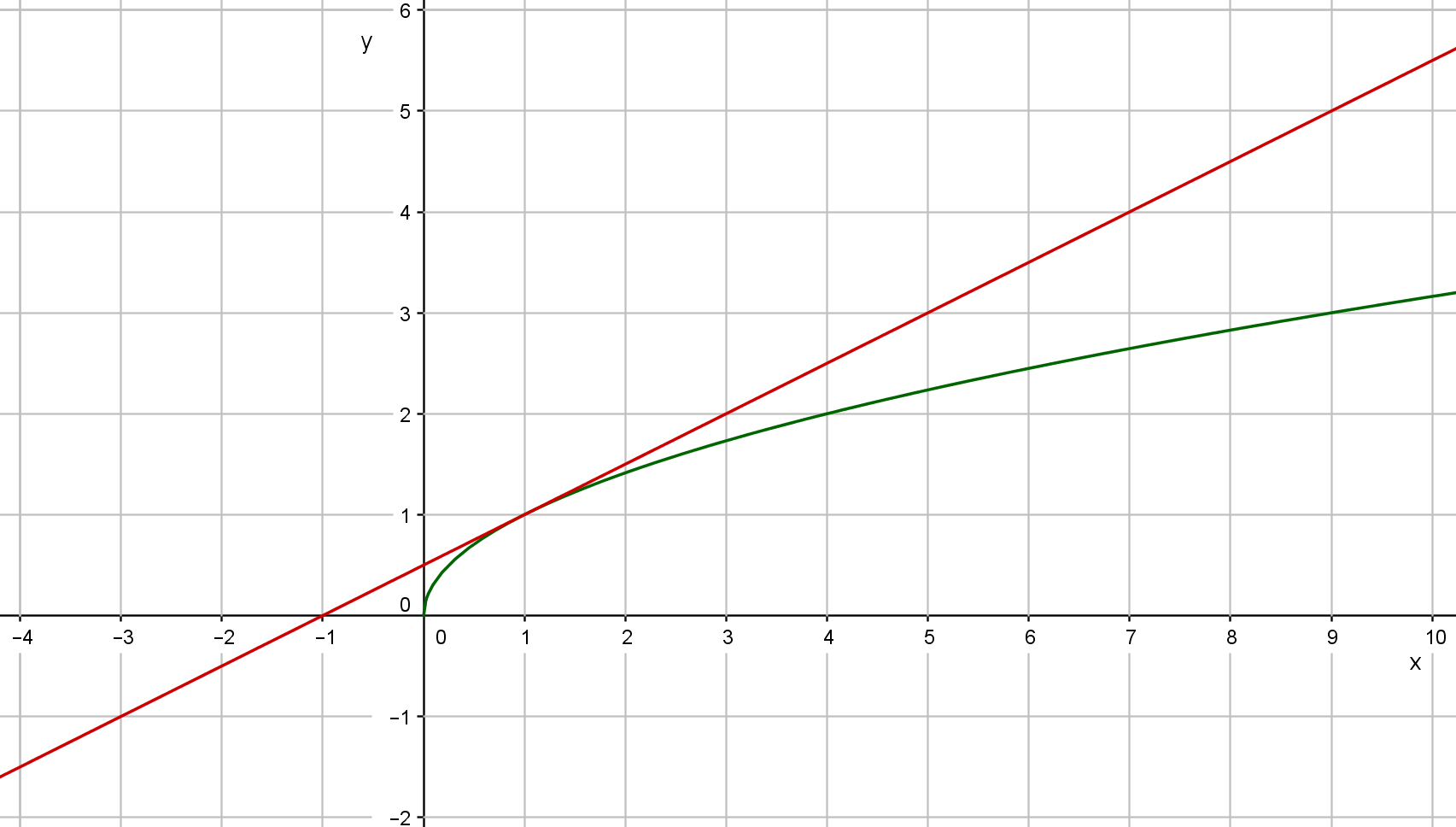
If we zoom in on the point $\rv{1,1}$ , we see that, at the point $x=1$ , the graph of $\sqrt{x}$ and the tangent line, which is given by the function $\frac{1}{2}x+\frac{1}{2}$ , are very close; see the figure below.

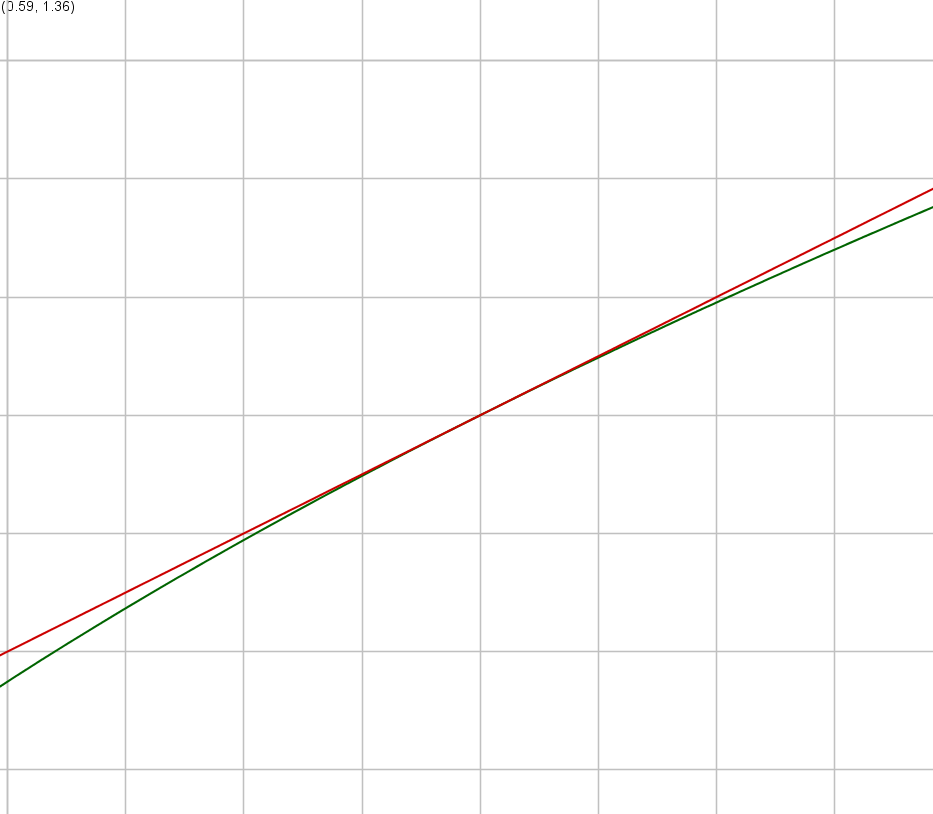
In particular, the value of the function of the tangent line at $x=1.1$ , the number $\frac{1}{2} \cdot 1.1+{1}{2}=1.05$ , is a good approximation of $\sqrt{1.1}$ . This is an example of the following tangent approximation formula.

Tangent approximation formula

Let $a$ be a point where the function $f$ is differentiable. If $h$ is chosen close enough to $0$ , then $f(a)+f'(a) \cdot h$ is a good approximation of $f(a+h)$ . In formula:

$f(a+h)\approx f(a)+f'(a) \cdot h\tiny.$

According to the definition of derivative: $f'(a)=\lim_{h \to 0} \frac{f(a+h)-f(a)}{h}$ .

This means that: $f'(a)\approx\frac{f(a+h)-f(a)}{h}$ .

This gives: $f(a+h)\approx f(a)+f'(a) \cdot h$ .

There are good estimations for the deviation from $f(a)+f'(a) \cdot h$ compared $f(a+h)$ , but we will not go into details here.

Using this formula, we can approximate the value of a differentiable function at points for which we would otherwise have needed a calculator.

Approximate the value of $\sqrt{x}$ at the point $1.14$ with the help of the tangent line approximation formula. Give your answer with a precision of $4$ decimal places.

$\sqrt{1.14}\approx$ $1.0700$

We use the tangent approximation formula. It states: $f(a+h)\approx f(a)+f'(a) \cdot h$ . Here $f(a)=\sqrt{x}$ , $a=1.0$ , and $h=0.14$ .

First, we calculate the derivative of $f$ using the power rule for differentiation: $f'(x)={{1}\over{2\cdot \sqrt{x}}}$ . Now we can enter the formula: $\sqrt{1.14}\approx f(1.0)+f'(1.0)\cdot 0.14 = \sqrt{1.0}+\frac{1}{2 \cdot \sqrt{1.0}} \cdot 0.14\approx 1.0700\tiny.$

For comparison: the precise approximation of $\sqrt{1.14}$ to four decimal places is: $1.0677$ .

New example