Functies: Kwadratische functies
 De abc-formule
De abc-formule
Door kwadraat af te splitsen kunnen we de kwadratische uitdrukking herschrijven tot
Discriminant en abc-formule
Laat , , reële getallen zijn met . De vergelijking kan herleid worden tot
De uitdrukking noemen we de discriminant van , en duiden we vaak aan met .
Met deze notatie geldt
- Als , dan zijn er geen oplossingen.
- Als , dan is er dus maar één oplossing: .
- Als , dan zijn er twee oplossingen.
Bovenstaande noemen we ook wel de abc-formule. Met deze formule is elke tweedegraads vergelijking op te lossen.
De herleiding gaat als volgt:
De abc-formule gebruiken we om de snijpunten van een parabool met de -as te bepalen. Wat betekent dit voor de drie gevallen die we net hebben gezien? We bekijken nu steeds een dalparabool.
Als , dan wordt de wortel getrokken uit een positief getal, zodat de vergelijking twee verschillende oplossingen heeft. De parabool, dat wil zeggen: de grafiek van , heeft snijpunten heeft met de -as.
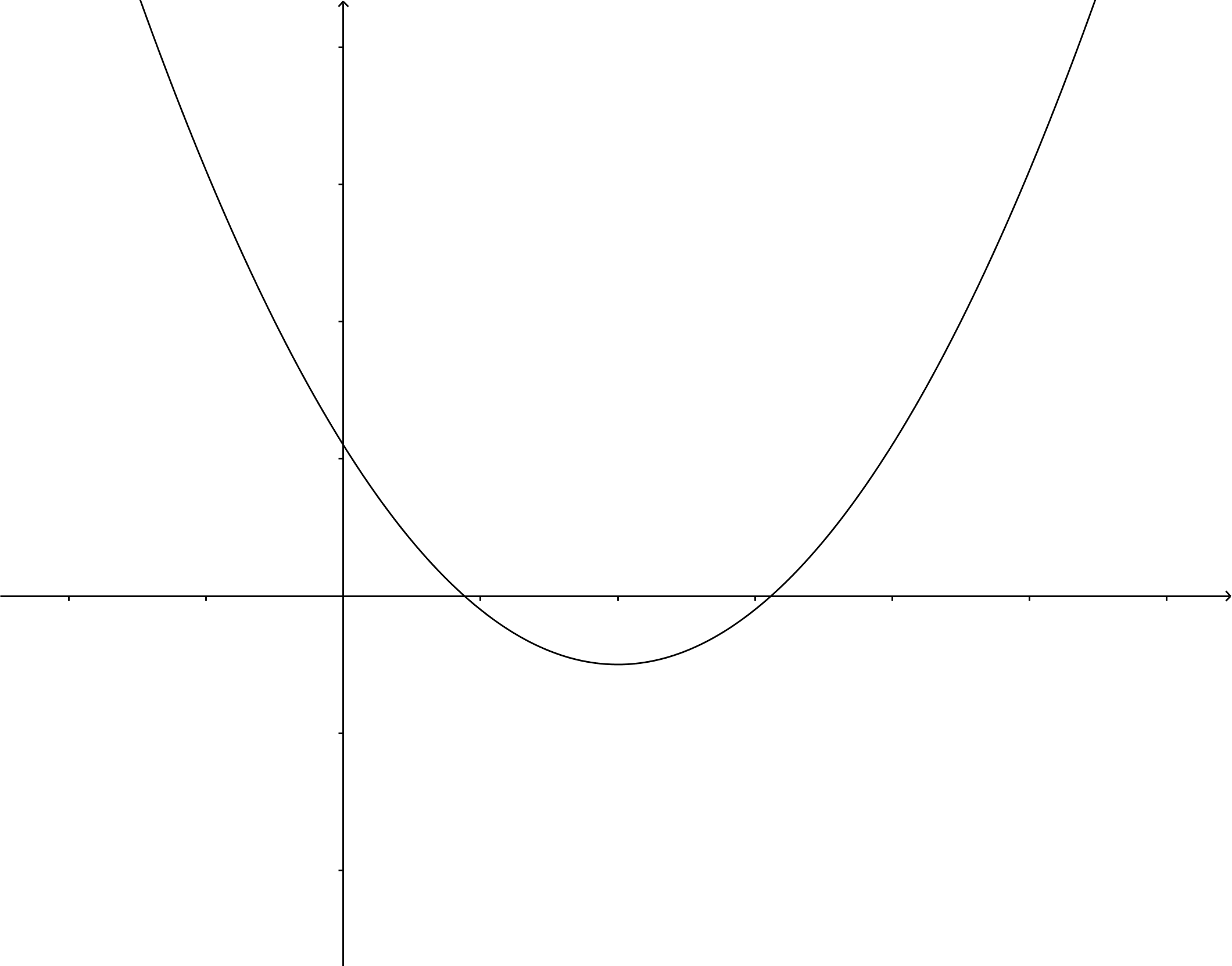
Als , dan zijn er geen oplossingen, omdat worteltrekken uit een negatief getal geen reëel getal oplevert. De parabool heeft dan geen snijpunten met de -as.
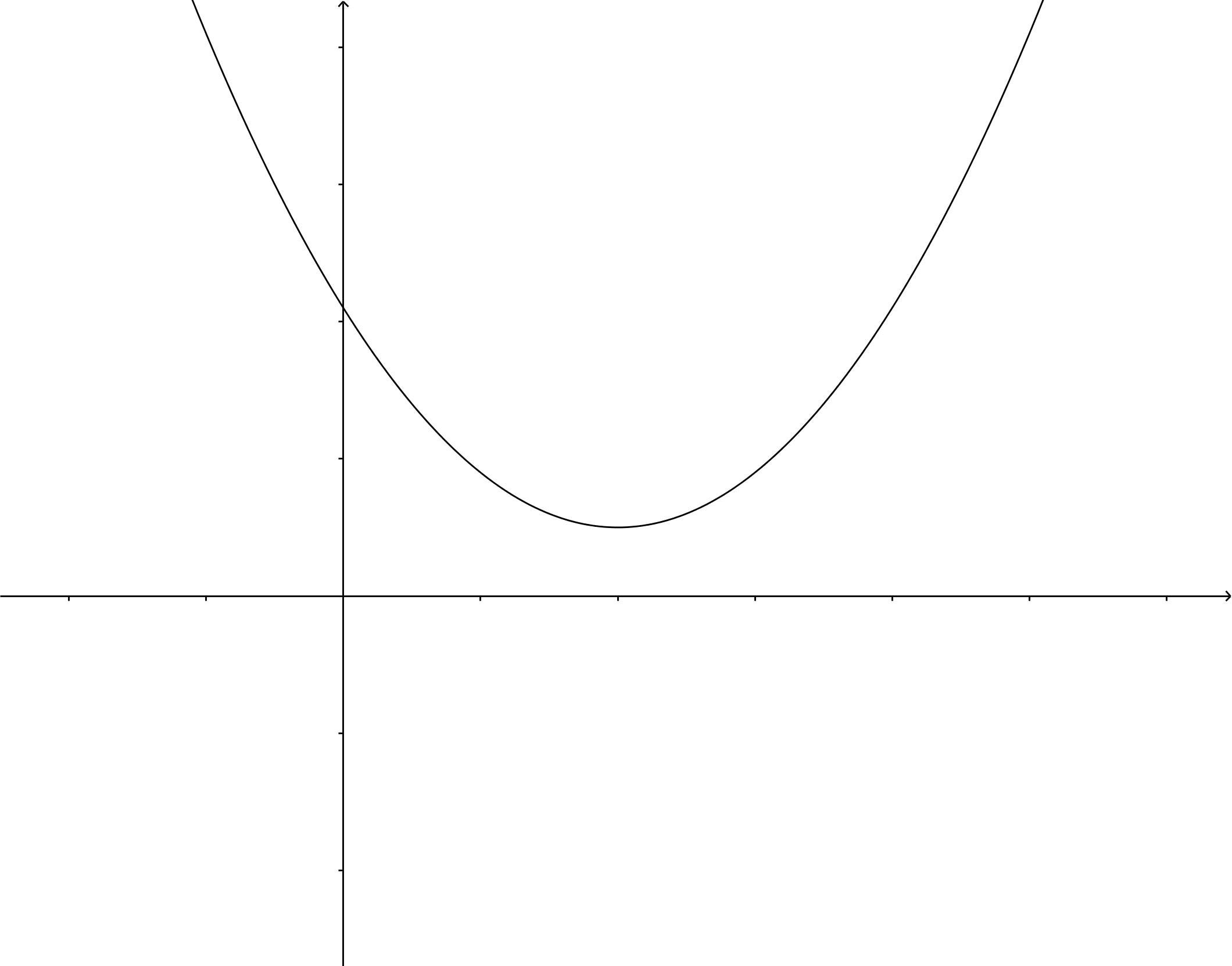
Als , dan zijn beide oplossingen gelijk en is er dus maar één oplossing: . Hier raakt de parabool de -as.
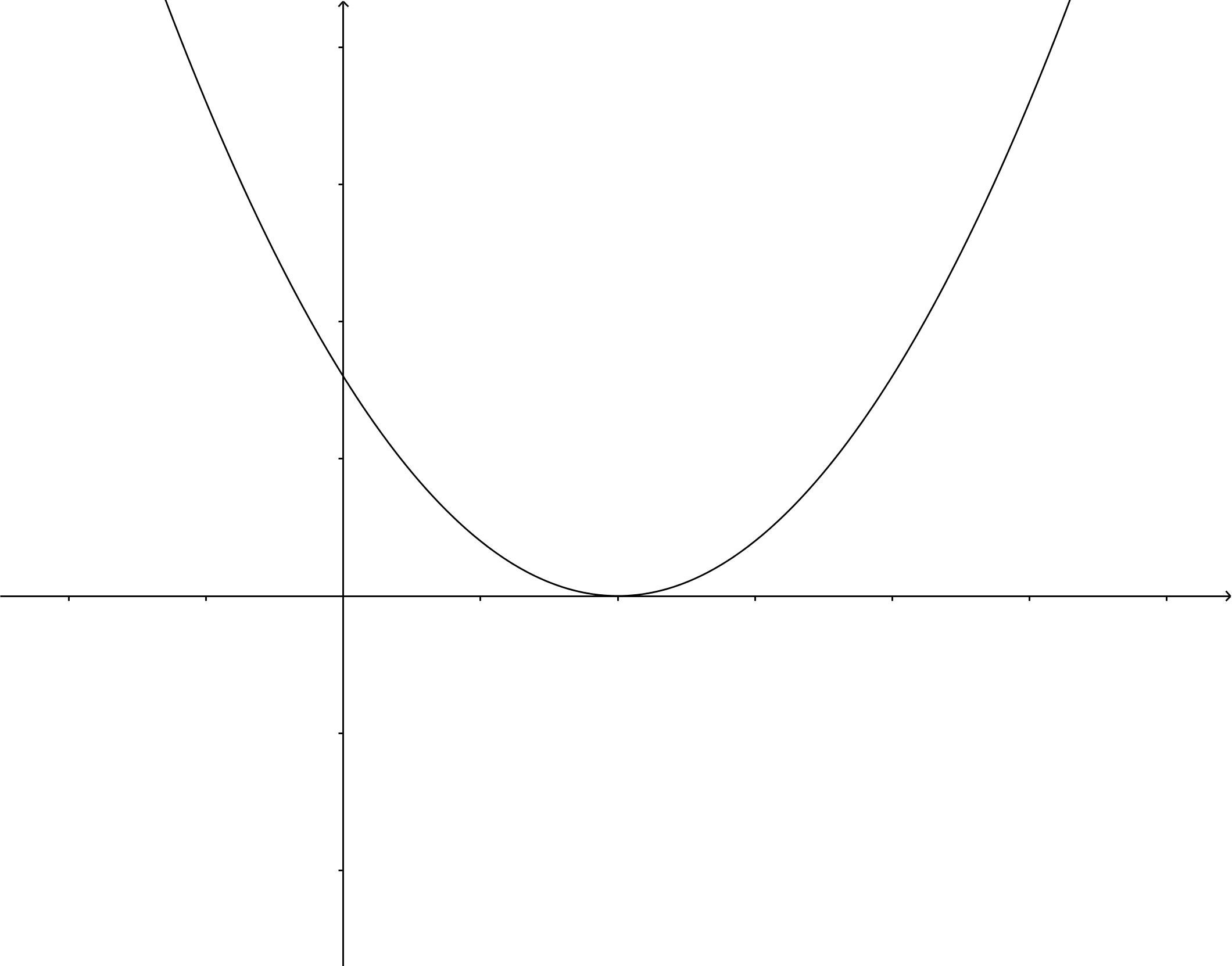
Maak gebruik van de abc-formule:
met discriminant .
De grafiek van de functie is hieronder getekend. De -coördinaten van de snijpunten van de grafiek met de -as zijn de oplossingen van de vergelijking.
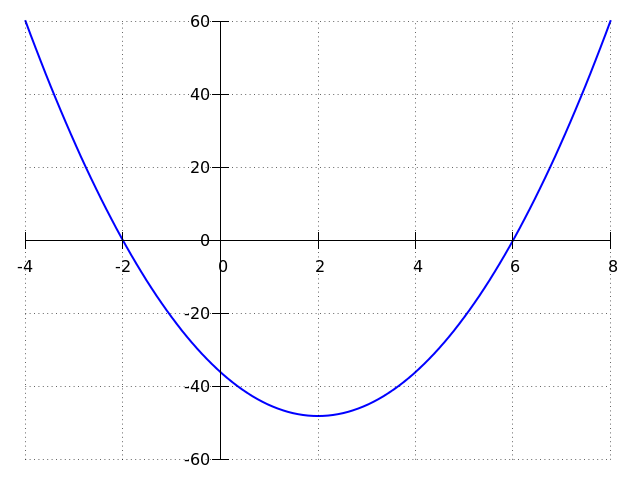

omptest.org als je een OMPT examen moet maken.



