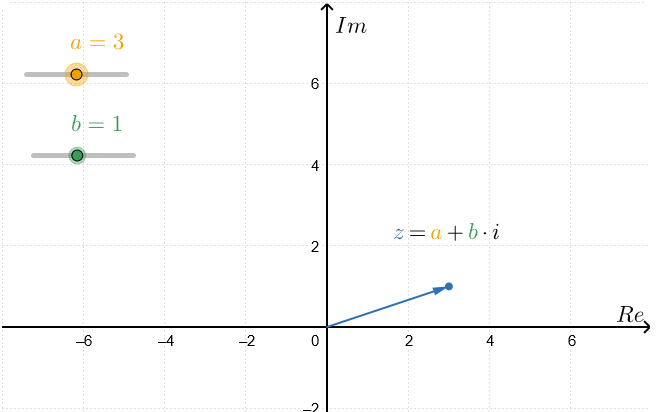Bewerkingen met complexe getallen: Rekenen met complexe getallen
 Complexe getallen
Complexe getallen
Complexe getallen zijn getallen met een algemene vorm #\blue{z}=\orange{a} + \green{b}\cdot\complexi# waarbij #\orange a# en #\green b# reëel zijn. Ze vormen de verzameling #\mathbb{C}# op dezelfde manier als reële getallen de verzameling #\mathbb{R}# vormen, rationale getallen de verzameling #\mathbb{Q}#, gehele getallen #\mathbb{Z}#, en natuurlijke getallen #\mathbb{N}#.
De cartesische vorm of standaardvorm van een complex getal #\blue{z}# is \[\blue{z}=\orange{a} + \green{b}\cdot\complexi\] waarbij #\orange a# en #\green b# reële getallen zijn.
Een complex getal heeft zowel een reëel deel, aangeduid als #\mathrm{Re}(z)#, als een imaginair deel, aangeduid met #\mathrm{Im}(z)#. \[\begin{array}{rcl}\mathrm{Re}(\blue z) &=& \orange{a}\\ \mathrm{Im}(\blue z) &=& \green{b}\end{array}\]
#\blue{z}# is puur imaginair als #\orange{a}=0# en #\green{b} \neq 0#
#\blue z# is reëel als #\green{b}=0#.
Voorbeelden
\[\begin{array}{rcl}
\blue{z} &=& \orange{1}+\green{\sqrt{2}} \cdot \ii \\
\blue{z} &=& \orange{-\frac{1}{2}}+\green{4} \cdot \ii
\end{array}\]
#\phantom{empty}#
\[\begin{array}{rcl}\blue{z} &=& \orange{-2}\green{-5} \cdot \ii \\
\mathrm{Re}(\blue z) &=& \orange{-2}\\ \mathrm{Im}(\blue z) &=& \green{-5}\end{array}\]
#\phantom{empty}#
\[\begin{array}{rcll}
\blue{z}&=&\green{7}\cdot \ii & \text{is puur imaginair} \\
\blue{z} &=& \orange{6} & \text{is reëel}
\end{array}\]
We kunnen dus zien dat de verzameling van reële getallen #\mathbb{R}# is bevat in de verzameling van complexe getallen #\mathbb{C}#, d.w.z. elk reëel getal kan worden weergegeven door een complex getal waarbij #\green{b}=0#.
De verzameling van alle complexe getallen #\mathbb{C}# kan worden weergegeven door een tweedimensionaal vlak met de horizontale as die overeenkomt met het reële deel van de complexe getallen, terwijl de verticale as overeenkomt met hun imaginaire deel. Dit is het zogenaamde Argand-diagram.
Laat #\blue{z}= \orange{a} + \green{b}\cdot\complexi#. In het Argand-diagram wordt dit getal weergegeven door een vector waarvan het eindpunt (de pijlpunt) de coördinaten #\rv{\orange{a},\green{b}}# heeft. Met andere woorden, de horizontale as geeft het reële deel van een complex getal aan, terwijl de verticale as het imaginaire deel aangeeft.
Het imaginaire deel van een complex getal #z = a + b\cdot \ii# is #b#. In dit geval geldt #b=-8#.

omptest.org als je een OMPT examen moet maken.