Varying duration, varying interest rate

Sequences and series: Financial applications of sequences and series

Varying duration, varying interest rate

Up to now we have calculated present and future values where the duration and interest rates are unchanged. That's not always the case in the real world. If we're dealing with a future or present value with varying duration, then in general it's only possible to calculate the future or present value by adding the future and present values of all individual terms.

There are exceptions. To express the calculations in these kinds of situations in the easiest way possible, we use a short notation, which we've seen before. We will repeat it here.

In this table we see the notations we've seen before.

Situation in which symbol occurred	Factor	Notation
Future value of periodic payments	#(1+i)^n#	#S_{\left .n\right \rceil i}#
Present value of periodic payments	#\frac{1}{(1+i)^n}#	#A_{\left .n\right \rceil i}#
Future value with annuity-immediate interest	#\frac{(1+i)^n-1}{i}#	#s_{\left .n\right \rceil i}#
Present value with annuity-immediate interest	#\frac{1-(1+i)^{-n}}{i}#	#a_{\left .n\right \rceil i}#
Future value with annuity-due interest	#(1+i) \cdot s_{\left .n\right \rceil i}#	#\ddot{s}_{\left .n\right \rceil i}#
Present value with annuity-due interest	#(1+i) \cdot a_{\left .n\right \rceil i}#	#\ddot{a}_{\left .n\right \rceil i}#

Here we see two examples in which we can compute the future value and present value relatively easy, although they have varying duration.

We can also take a look at situations in which the duration is unchanged, but the interest varies over the duration. In the case when the interest per interval stays the same, the future and present value can be calculated. You'll also see such an example here.

Finally, we'll also take a look at an example in which both the duration as well as the interest rates vary.

A company expects the following cash flow the next years: the first #3# years #\euro \, 1# million per year and in years #4# through #8# a cash flow of #\euro \, 1.4# million.

With the goal of comparing these cash flows with new capital investment, the present value of the cash flows is determined. The interest rate is #3.9\%# per year.

Enter the present value. Give your answer in million euro's, precise up to one hundred thousand euro.

The present value is: #\euro# #8.4# million

There are two simple methods on how to approach this exercise. The first one uses the sum of two present values that can be calculated with a known formula. The second one works with a difference. We will describe both methods by means of timelines.

Method 1

We will now calculate the sum of the following two amounts:

the present value of #3# year with a term of #\euro \, 1# million and a growth rate of #i=\frac{3.9}{100}=0.039#
the present value for #5# year with a term of #\euro \, 1.4# million and a growh rate of #i=\frac{3.9}{100}=0.039# divided by the #3#th power of the growth factor.

In a formula it looks like this:
\[PV=1 \cdot a_{\left .3\right \rceil 0.039} + 1.4 \cdot a_{\left .5\right \rceil 0.039} \cdot A_{\left .3\right \rceil 0.039}\]
Which gives us
\[PV = 1 \cdot \frac{1-{1.039}^{-3}}{0.039}+1.4 \cdot \frac{1-{1.039}^{-5}}{0.039} \cdot \frac{1}{{1.039}^{3}}=8.353\]

Method 2

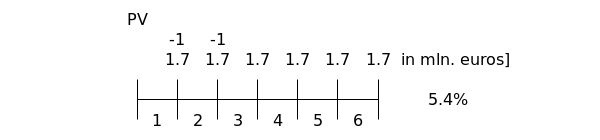
Now we calculate the present value as the difference of the following two amounts

calculate the present value of the total of #8# years with terms #\euro \, 1.4# million with an interest rate of #3.9\%#
the present value of #3# year a term of #\euro \, -0.4# million with an interest rate of #3.9\%# per year

In a formula it looks like this:
\[PV=1.4 \cdot a_{\left .8\right \rceil 0.039} -0.4 \cdot a_{\left .3\right \rceil 0.039}\]
Which gives us
\[PV = 1.4 \cdot \frac{1-{1.039}^{-8}}{0.039} -0.4 \cdot \frac{1-{1.039}^{-3}}{0.039}=8.353\]

Hence, the present value is #\euro \, 8.4# million.

New example