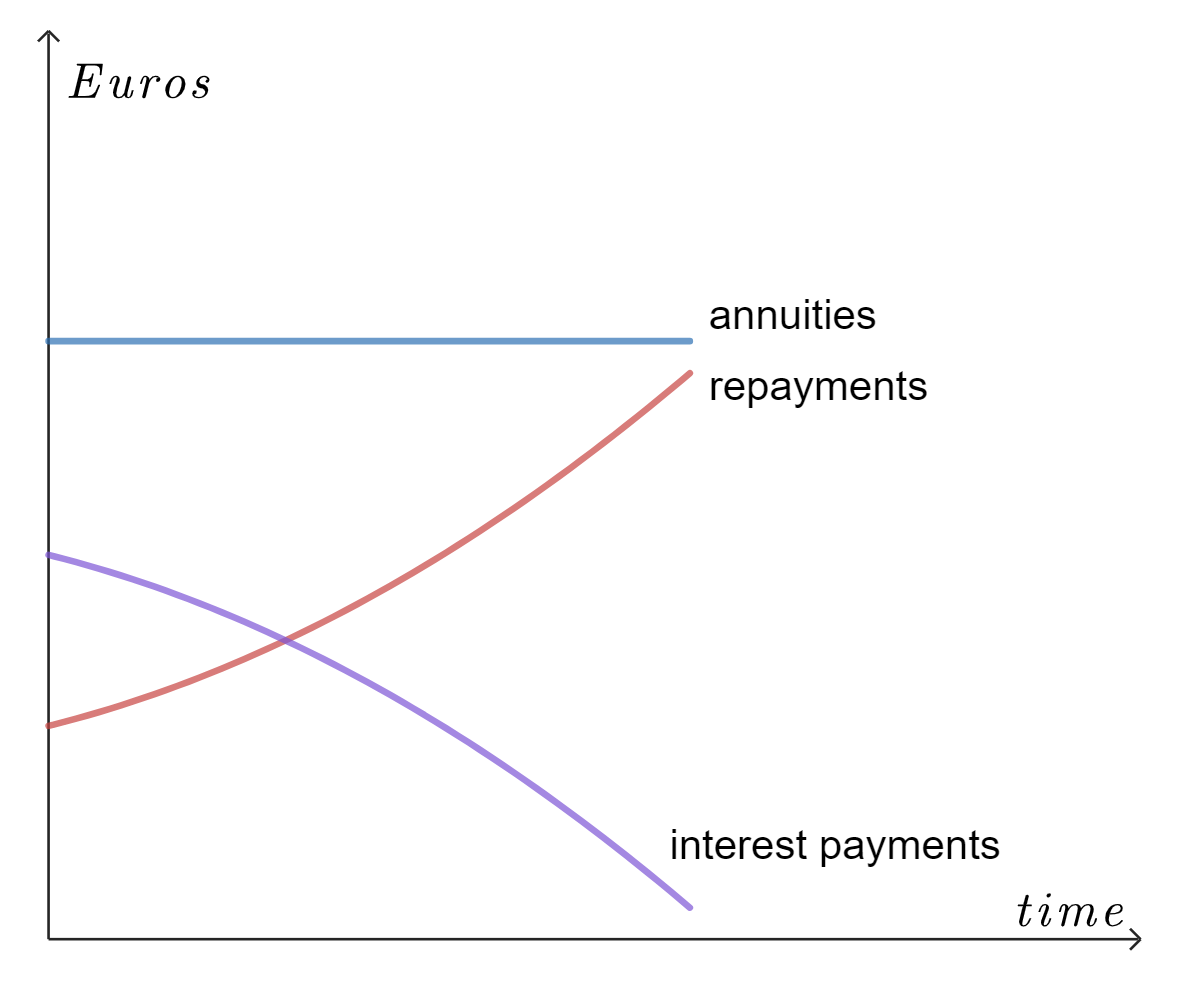
The defining characteristic of an annuity loan is the fact that total payments per term stay constant the entire duration of the loan. This means that the amount of the interest payment and the amount of the installment needs to be chosen in such a way that the sum of these payments leads to the same amount each term. This amount is called the annuity, and is indicated with #Ann#.
The annuity satisfies:
\[\begin{array}{rcl}Ann &=& \dfrac{C\cdot i}{1-(1+i)^{-n}}\\&=& r_j +a_j\\\end{array}\]
Hence, an annuity loan satisfies the following formulas:
\[\begin{array}{rcl}\text{Installments }&&a_1 =\dfrac{C\cdot i}{(1+i)^n-1} \\ &&a_j = a_1\cdot (1+i)^{j-1}\\ &&\sum_{}a_j = C \\ \text{Interest payments }&&r_j = Ann - a_j\\ \text{Remaining debt }&&R_j = C\cdot \dfrac{1-(1+i)^{j-n}}{1-(1+i)^{-n}}\\ \end{array}\]
Just as with a linear loan, at the end of each term a part of the debt is paid off, resulting in a lower interest payment the following term. At the beginning of the duration the installments are relatively small, but this amount increases as time passes.
#a_1 \lt a_2 \lt a_3 \lt \cdots \lt a_n#
#r_1 \gt r_2 \gt r_3 \gt \cdots \gt r_n#
An 10%-annuity loan of €100,000 with a duration of 10 years leads to the following payments table.
| Term |
Debt begin |
Annuity |
Interest payment |
Installment |
Debt end |
| #j# |
#R_{j-1}# |
#Ann# |
#r_j# |
#a_j# |
#R_j# |
| 1 |
100,000.00 |
16,274.54 |
10,000.00 |
6,274.54 |
93,725.46 |
| 2 |
93,725.46 |
16,274.54 |
9,372.55 |
6,901.99 |
86,823.47 |
| 3 |
86,823.47 |
16,274.54 |
8,682.35 |
7,592.19 |
79,231.27 |
| 4 |
79,231.27 |
16,274.54 |
7,923.13 |
8,351.41 |
70,879.86 |
| 5 |
70,879.86 |
16,274.54 |
7,087.99 |
9,186.55 |
61,693.31 |
| 6 |
61,693.31 |
16,274.54 |
6,169.33 |
10,105.21 |
51,588.10 |
| 7 |
51,588.10 |
16,274.54 |
5,158.81 |
11,115.73 |
40,472.37 |
| 8 |
40,472.37 |
16,274.54 |
4,047.24 |
12,227.30 |
28,245.07 |
| 9 |
28,245.07 |
16,274.54 |
2,824.51 |
13,450.03 |
14,795.04 |
| 10 |
14,795.04 |
16,274.54 |
1,479.50 |
14,795.04 |
0 |
In a graph:
We will assume the fact that each term a fixed amount is paid. This amount is #a_j+r_j# for term #j#. We will first show that the installments #a_j# of an annuity loan in the terms #j=1,2,\ldots# form a geometric sequence with scale factor #(1+i)#:
\[\begin{array}{lclcc}
&&Ann = r_j + a_j = r_{j+1} + a_{j+1} &(1)&\\
&&\phantom{xxxxxxx}\color{blue}{\text{characterizing formula annuity }}\\
&&r_j = i \cdot R_{j-1} &(2)&\\
&&\phantom{xxxxxxx}\color{blue}{\text{formula interest payments term } j}\\
&&r_{j+1} = i \cdot R_j = i \cdot (R_{j-1} - a_j) = i\cdot R_{j-1} - i\cdot a_j &(3)&\\
&&\phantom{xxxxxxx}\color{blue}{\text{formula interest payments term }j + 1}&&\\
&&i\cdot R_{j-1} + a_j = i\cdot R_{j-1} - i\cdot a_j + a_{j+1}&&\\
&&\phantom{xxxxxxx}\color{blue}{\text{(2) and (3) entered in second equality (1)}}&&\\
&&a_{j+1}=a_j+i\cdot a_j\\
&&\phantom{xxxxxxx}\color{blue}{\text{the previous equation simplified }}&&\\
&& a_{j+1}=a_j\cdot (1+i) &&\\
&&\phantom{xxxxxxx}\color{blue}{a_j\,\,\text{moved outside brackets }}&&\\
\end{array}\]
This indeed shows #a_j=a_1\cdot (1+i)^{j-1}#. To determine #a_1#, we use the fact that the sum of all installments is equal to the initial borrowed capital #C#:
\[\begin{array}{rcl}C&=&\sum_{j=1}^na_j \\ &=&a_1\cdot\sum_{j=1}^n{(1+i)^{j-1}} \\ &&\phantom{xx}\color{blue}{a_j = a_1\cdot (1+i)^{j-1}}\\ &=&a_1\cdot\dfrac{(1+i)^{n}-1}{1+i-1} \\ &&\phantom{xx}\color{blue}{\text{geometric sequence}}\\ &=&a_1\cdot\dfrac{(1+i)^{n}-1}{i}\end{array}\]
Hence, we find the linear equation #a_1\cdot\dfrac{(1+i)^{n}-1}{i}=C# with unknown #a_1#, leading to
\[a_1 = \dfrac{C\cdot i}{(1+i)^n-1}\]
Now that we know all #a_j#, we calculate the remaining debts #R_j# as follows:
\[\begin{array}{rcl}
R_j &=& R_{j-1}-a_j = R_{j-2}-a_{j-1}-a_j=\cdots\\ &=&R_0-a_1-a_2-\cdots-a_j\\ &=&C-a_1\cdot\left(1+(1+i)+(1+i)^2+\cdots+(1+i)^{j-1}\right)\\ &=&C-a_1\cdot \dfrac{(1+i)^j-1}{i}\\ &&\phantom{xxxxxxx}\color{blue}{\text{geometric sequence }}\\&=&C- \dfrac{C\cdot i}{(1+i)^n-1}\cdot \dfrac{(1+i)^j-1}{i}\\ &&\phantom{xxxxxxx}\color{blue}{\text{formula for }a_1\text{ entered }}\\&=&C- \dfrac{C\cdot \left((1+i)^j-1\right)}{(1+i)^n-1}\\&&\phantom{xxxxxxx}\color{blue}{\text{fractions multiplied }}\\ &=&C\cdot\dfrac{(1+i)^n-1- \left((1+i)^j-1\right)}{(1+i)^n-1}\\&&\phantom{xxxxxxx}\color{blue}{\text{everything on the right hand side brought over one denominator }} \\&=& C\cdot \dfrac{1-(1+i)^{j-n}}{1-(1+i)^{-n}}\\
&&\phantom{xxxxxxx}\color{blue}{\text{fraction simplified}}
\end{array}\]
The interest payments #r_j# are directly related to the remaining debts:
\[
r_j = i\cdot R_{j-1}= i\cdot C\cdot \dfrac{1-(1+i)^{j-1-n}}{1-(1+i)^{-n}}
\]
We indeed conclude that #Ann=a_j+r_j# is constant (meaning: not being dependent on #j#) for the found values of #a_j# and #r_j#:
\[\begin{array}{rcl}
a_j+r_j &=&a_1\cdot (1+i)^{j-1}+i\cdot C\cdot \dfrac{1-(1+i)^{j-1-n}}{1-(1+i)^{-n}}\\&&\phantom{xxxxxxx}\color{blue}{\text{formulas for }a_j\text{ and }r_j\text{ entered }} \\ &=& \dfrac{C\cdot i}{(1+i)^n-1}\cdot (1+i)^{j-1}+i\cdot C\cdot \dfrac{(1+i)^n-(1+i)^{j-1}}{(1+i)^{n}-1}\\ &&\phantom{xxxxxxx}\color{blue}{\text{formula for}a_1\text{ entered }}\\ &=& C\cdot i\cdot \dfrac{ (1+i)^{j-1}+ (1+i)^n-(1+i)^{j-1}}{(1+i)^{n}-1}\\ &&\phantom{xxxxxxx}\color{blue}{\text{like fractions added }}\\ &=& C\cdot i\cdot \dfrac{ (1+i)^n}{(1+i)^{n}-1}\\&&\phantom{xxxxxxx}\color{blue}{\text{terms with }j\text{ cancel out }}\\ &=&\dfrac{C\cdot i}{1-(1+i)^{-n}}\\&&\phantom{xxxxxxx}\color{blue}{\text{numerator and denominator divided by }(1+i)^n} \end{array}\]
The last expression is the formula for#Ann# in the theorem.
The formula for the annuity #Ann# can also be derived by thinking of #Ann# as the present value of an annuity-immediate interest with fixed terms:
\[\begin{array}{rcl}
a_{\left .n\right \rceil i} &=& \dfrac{1-(1+i)^{-n}}{i}\\
&&\phantom{xxxxxxx}\color{blue}{\text{formula present value factor }}\\
Ann &=& \dfrac{C}{a_{n|i}}\\
&&\phantom{xxxxxxx}\color{blue}{\text{formula annuity}}\\
&=& \dfrac{C}{\dfrac{1-(1+i)^{-n}}{i}}\\
&&\phantom{xxxxxxx}\color{blue}{a_{n|i}\,\,\text{entered}}\\
&=& C \cdot \dfrac{i}{1-(1+i)^{-n}}\\
&&\phantom{xxxxxxx}\color{blue}{\text{dividing by a fraction is multiplying by the reverse}}\\
&=& \dfrac{C\cdot i}{1-(1+i)^{-n}}\\
&&\phantom{xxxxxxx}\color{blue}{\text{simplified}}\\
\end{array}\]
Reduction of the formula for calculating the remaining debt:
\[\begin{array}{rcl}
R_j &=& Ann \cdot a_{n-j|i}\\
&&\phantom{xxxxxxx}\color{blue}{\text{formula remaining debt annuity loan}}\\
&=&\dfrac{C\cdot i}{1-(1+i)^{-n}}\cdot \dfrac{1-(1+i)^{-(n-j)}}{i}\\
&&\phantom{xxxxxxx}\color{blue}{Ann\,\text{ and }a_{n-j|i}\,\text{entered}}\\
&=& C\cdot \dfrac{1-(1+i)^{j-n}}{1-(1+i)^{-n}}\\
&&\phantom{xxxxxxx}\color{blue}{\text{simplified}}\\
\end{array}\]
Given a 7%-annuity loan of #\euro\,##100000# with a duration of #15# years. The interest rate given is a yearly percentage.
Calculate the annuity of this loan with monthly payments, rounded to two decimals.
Monthly annuity #=# #886.85#
Given:
- initial borrowed capital: #C = 100000#
- growth rate: #i =i_{\text{year}} = 0.07#
- duration: #n =n_{\text{year}} = 15#
To calculate the requested annuity, we must first determine the interest per month and the duration in months. Both use the fact that a year consists of 12 months.
According to a conversion formula for growth rates, following from the
conversion formula for growth factors,
we have for the monthly growth rate \[i_{\text{month}} = \left(1+i_{\text{year}}\right)^{\frac{1}{12}} - 1\approx 0.00565415\]
Moreover, for the duration we have \[i_{\text{month}} = 12\cdot 15 = 180 \]
The monthly annuity is calculated as follows:
\[\begin{array}{rcl}
Ann_{\text{month}} &=& \dfrac{C\cdot i_{\text{month}}}{1-(1+i_{\text{month}})^{-n_{\text{month}}}}\\
&&\phantom{xxxxx}\color{blue}{\text{the formula for the annuity}}\\
&\approx & \dfrac{100000\cdot 0.00565415}{1-(1+0.00565415)^{-180}}\\
&&\phantom{xxxxx}\color{blue}{\text{values for }C, i_{\text{month}}\text{ and }n_{\text{month }}\text{ entered}}\\
&\approx& 886.85\\
&&\phantom{xxxxx}\color{blue}{\text{calculated}}\\
\end{array}\]
 Annuities
Annuities





